An aesthetic appreciation of mathematical dimensions.

When we talk about dimensions are they just another technical stuff that learners need to memorize?

Before answering that question, here is an activity. What can you make by folding the lines & gluing the edges of these 2D shapes?

You just used a 2D pattern to fold it back to its 3D structure. Such 2D patterns are called nets. Here are few more such patterns. 

Have a look at the 4th dimensional analogue of a cube. It invites your awe. It is called a tesseract ( a cube in a cube).

Like our earlier geometric nets, when a 4D tesseract unfolded into its 3D net it will look like.

Painting on a (2D) surface doesn't give much scope to explore, they say. Well, they haven't heard of Salvador Dali. He was a prominent Spanish surrealist painter. His work, like that of M C Escher exhibit many interesting mathematical ideas. The progression from a non-dimensional point to the 4th dimensional tesseract and back couldn't have left an artist of his genius uninspired. He took the tesseract net

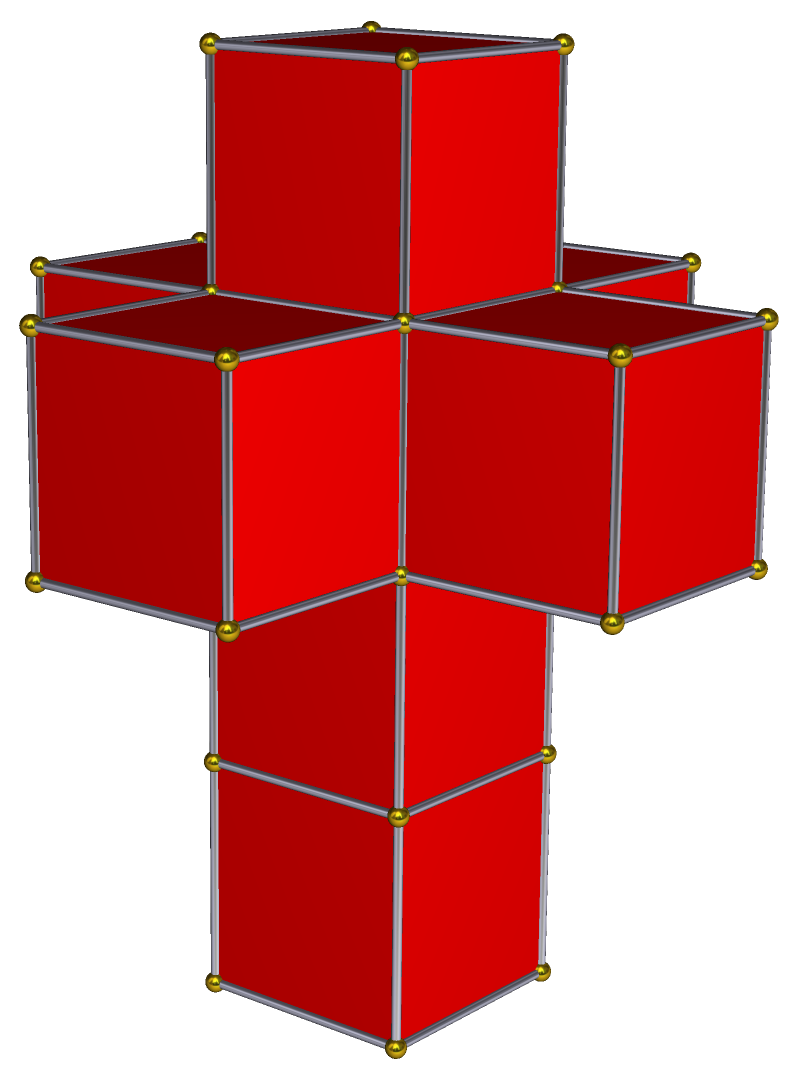
and from there was born his masterpiece Crucifixion. "Instead of painting Christ on a wooden cross, Dalí depicts him upon the net of a hypercube, also known as a tesseract. The unfolding of a tesseract into eight cubes is analogous to unfolding the sides of a cube into six squares."

With Dali, the master surrealist there is lot more to explore in contemporary mathematical ideas and scientific discoveries. "Dalí's homage to Isaac Newton, with an open torso and suspended heart to indicate "open-heartedness," and an open head indicating "open-mindedness"—the two very qualities important for science discovery and successful human endeavours."

That's another story, another dimension!